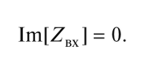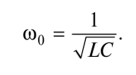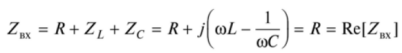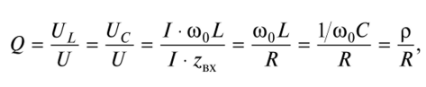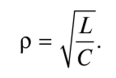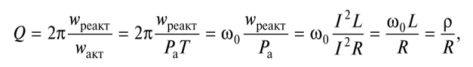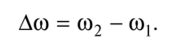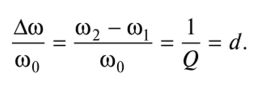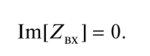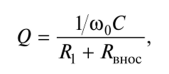當電感性元件與電容性元件串聯(lián)連接時，電路中的諧振稱為電壓諧振，而該電路稱為串聯(lián)諧振或變頻諧振電路。在圖顯示了最簡單的時序電路，發(fā)生諧振的條件是等式，等于電路總電抗為零（輸入復數(shù)電阻的虛部）：

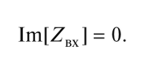
從線圈和電容器的電抗相等，很容易獲得發(fā)生諧振的頻率值（co 0）：

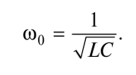
在這種情況下，電路的總輸入阻抗將是純電阻性的：

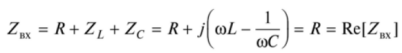
且在0至0的頻率范圍內(nèi)具有最小值。因此，電路中的輸入電流將在諧振時精確最大。

借助于串聯(lián)諧振電路，可以降低低頻（co <co t）和高頻（co> co 2）信號的幅度，即 該電路是一個中檔濾波器。濾波的質(zhì)量取決于頻率響應和相位響應圖的陡峭程度-曲線越陡峭，濾波器分配的頻率范圍就越窄。

為了確定諧振電路的頻率選擇特性，需要使用三個參數(shù)，其物理含義是相同的-頻率響應曲線斜率的數(shù)字描述。這些是品質(zhì)因數(shù)Q，帶寬Dco和衰減d。

品質(zhì)因數(shù)Q定義為諧振時電抗元件兩端電壓的有效值與輸入電壓的有效值之比：

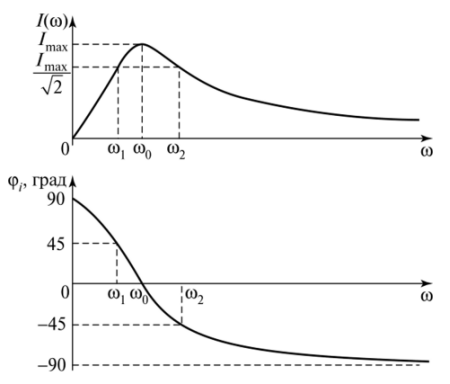
串聯(lián)諧振電路電流的頻率響應和相位響應

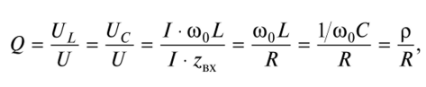
其中z BX是電路在諧振頻率下的輸入電阻的模數(shù)；p-波阻。特征阻抗是在輸入動作的特定波長（頻率）下電抗元件的復阻抗的模量。對于振蕩電路，這是諧振頻率。

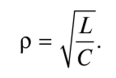
隨著有源電阻R和電容器C的電容的增加，串聯(lián)諧振電路的Q因數(shù)減小，即。頻率響應圖變得更平坦。隨著電感的增加，線圈變得更陡峭。

從能量的角度來看，諧振電路的Q因子是一個值，該值與諧振電路的電磁能量供應與輸入動作期間有源電阻中以熱量形式釋放的能量之比成正比：

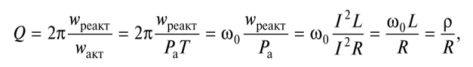
其中w peakt是在輸入動作期間在線圈或電容器上累積的能量；作用是在輸入作用期間在有源電阻上以熱量形式釋放的能量；? 一個 -有功功率。

諧振電路Dco的帶寬是輸出信號功率的值至少是輸入信號功率的一半的頻率范圍。如果我們從功率轉到諧振電路的輸入電流，則可知通帶內(nèi)串聯(lián)諧振電路中的電流不小于。

在諧振電路的通帶邊界處，電流和輸入電壓之間的相移值為φgran =±45°。頻率W0 和W2分別稱為通帶的截止頻率。

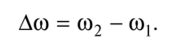
在這種情況下，

衰減d是品質(zhì)因數(shù)Q的倒數(shù)。

帶寬，Q因子和衰減之間的關系如下：

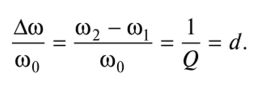
串聯(lián)諧振電路的Q系數(shù)越高，其帶寬越窄。

上面獲得的所有公式僅適用于最簡單的無負載串聯(lián)諧振電路。考慮將一個電阻與一個電抗元件之一并聯(lián)時的電路。

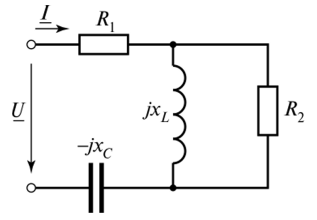
負載諧振電路

圖所示電路中發(fā)生諧振的條件 是輸入電阻的虛部等于零：

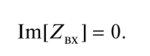
諧振頻率的值不僅取決于電抗元件L和C 的參數(shù)，而且取決于有源電阻R 2。

負載諧振電路的品質(zhì)因數(shù)由下式確定

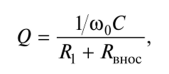
從中可以看出，負載電路的質(zhì)量因數(shù)低于未負載電路的質(zhì)量因數(shù)。